Daisuke Miki
Faculty of Culture and Information Science, Doshisha University
Akihiro Kawase
Faculty of Culture and Information Science, Doshisha University
Daisuke Miki
Faculty of Culture and Information Science, Doshisha University
Akihiro Kawase
Faculty of Culture and Information Science, Doshisha University
The compositional style of Ludwig van Beethoven (1770-1827) has conventionally been divided into three periods. According to Lenz (1855), who divided Beethoven’s compositional style for the first time, the first, second, and third periods are respectively the periods that span from 1794 to 1800, 1801 to 1814, and 1814 to 1827. Several other musicologists, such as Bücken (1931), Schenk (1967), Moroi (1983), and Hirano (2012), have proposed different divisions. However, past musicologists do not share a common understanding of how to divide Beethoven’s compositional style.
This situation could cause confusion about the stylistic evolution of Beethoven’s music. The divisions in Beethoven’s compositional style were not originally made from the viewpoint of musical theory, but instead based on major turning points in his biography. Therefore, recent researchers have conducted quantitative analyses to identify the specific features that characterise each period.
Richard (2011) found that the differences between the three periods of Beethoven’s works can be explained by the contrast of intensity in dynamics, tempo, and harmony. Furthermore, Honingh and Bod (2011) revealed that the tritone interval category (IC) is an effective feature by which to perform discriminant analysis to determine the periods in Beethoven’s works. However, it is still unclear what specific types of chords and harmonic progressions are unique in each period.
This study aims to clarify the periodisation boundaries in his compositional style and determine the specific features that distinguish one period from another. In this study, we applied supervised learning to the relative frequency of N-gram extracted from Beethoven’s all-string quartets (16 pieces; 70 movements) in terms of harmony, melody, and rhythm. We chose the string quartets as our sample because Beethoven composed in this genre throughout his career.
We conducted a discriminant analysis using decision trees and random forests to build a model that distinguishes in which period the piece was composed. Several decision trees have been generated to visualise the classification process. The importance of various features is measured by the value of Mean Decrease Gini (MDG) that is calculated in the random forests.
As a result of the comparison of the OOB error rates (Table 1), the models using harmonic and melodic features turned out to have better accuracy than the one using rhythmic features. Table 2 shows the OOB error rates of the models that combine several feature variables type. The discriminant models with harmonic and melodic features achieved the best accuracy. Among two-period-models, the first and the third periods work the best as the target categories.
Table 1: OOB error rate of each models
| Feature variables type | unigram | bigram | trigram | fourgram |
|---|---|---|---|---|
| Harmony | 0.3429 | 0.3429 | 0.4286 | – |
| Melody | 0.4000 | 0.3429 | 0.4000 | – |
| Rhythm | 0.6857 | 0.6429 | 0.7143 | – |
Table 2: OOB error rate of each models
| Feature variables type | period 1 / 2 / 3 | period 1 / 3 | period 1 / 2 | period 2 / 3 |
|---|---|---|---|---|
| Harmony (unigram + bigram) | 0.3571 | 0.1800 | 0.2727 | 0.4565 |
| Harmony + Melody | 0.2857 | 0.0800 | 0.3182 | 0.3913 |
| Harmony + Melody + Rhythm | 0.3286 | 0.1600 | 0.2727 | 0.4130 |
We found out that the important harmonic features for the classification are the relative frequencies of transition from the double dominant ninth chord with the root note omitted to the dominant chord (#viio7/V – V), the progression from the dominant seventh chord to the tonic chord (V7 – I), and the second inversion of the dominant seventh chord (V34). The important melodic features turned out to be the major second descent followed by the perfect fifth descent, the continuous chromatic ascent, and the repeat of same note after the minor third ascent.
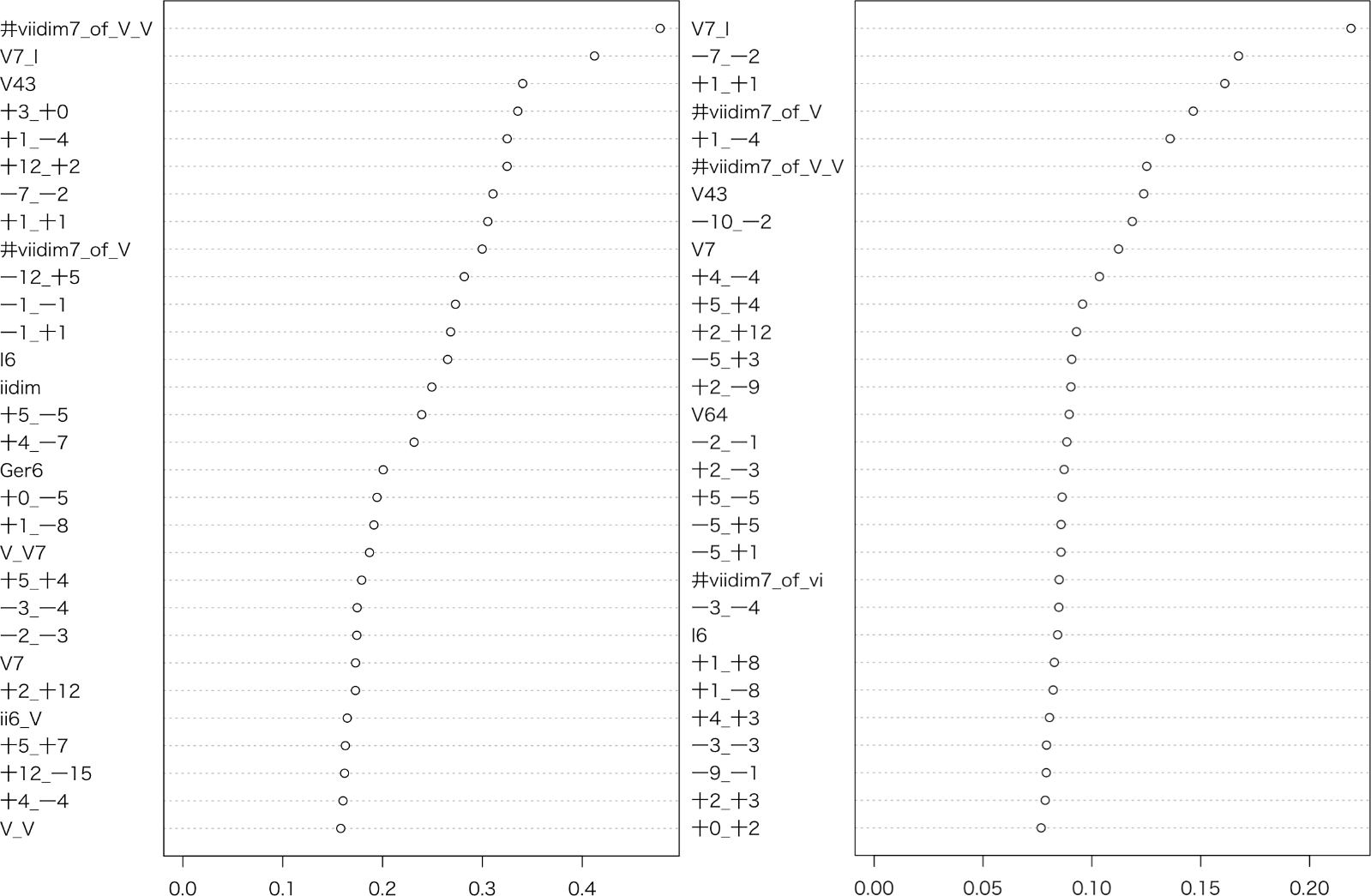
Figure 2 is the visualisation of the classification process generated with a decision tree for three periods. The relative error rate for this decision tree is 0.0227. The criteria for the discrimination of the works composed in the first period are high frequency of transition from the double dominant ninth chord with the root note omitted to the dominant chord, the scarcity of major second descent followed by perfect fourth descent, the scarcity of the second inversion of submediant chord, and the abundance of chromatic ascent after chromatic descent. The chord that discriminates the second period is the high frequency of the first inversion of the tonic chord. Furthermore, the feature that sets the third period apart is the transition from the first inversion of the tonic chord to the first inversion of the dominant seventh chord.
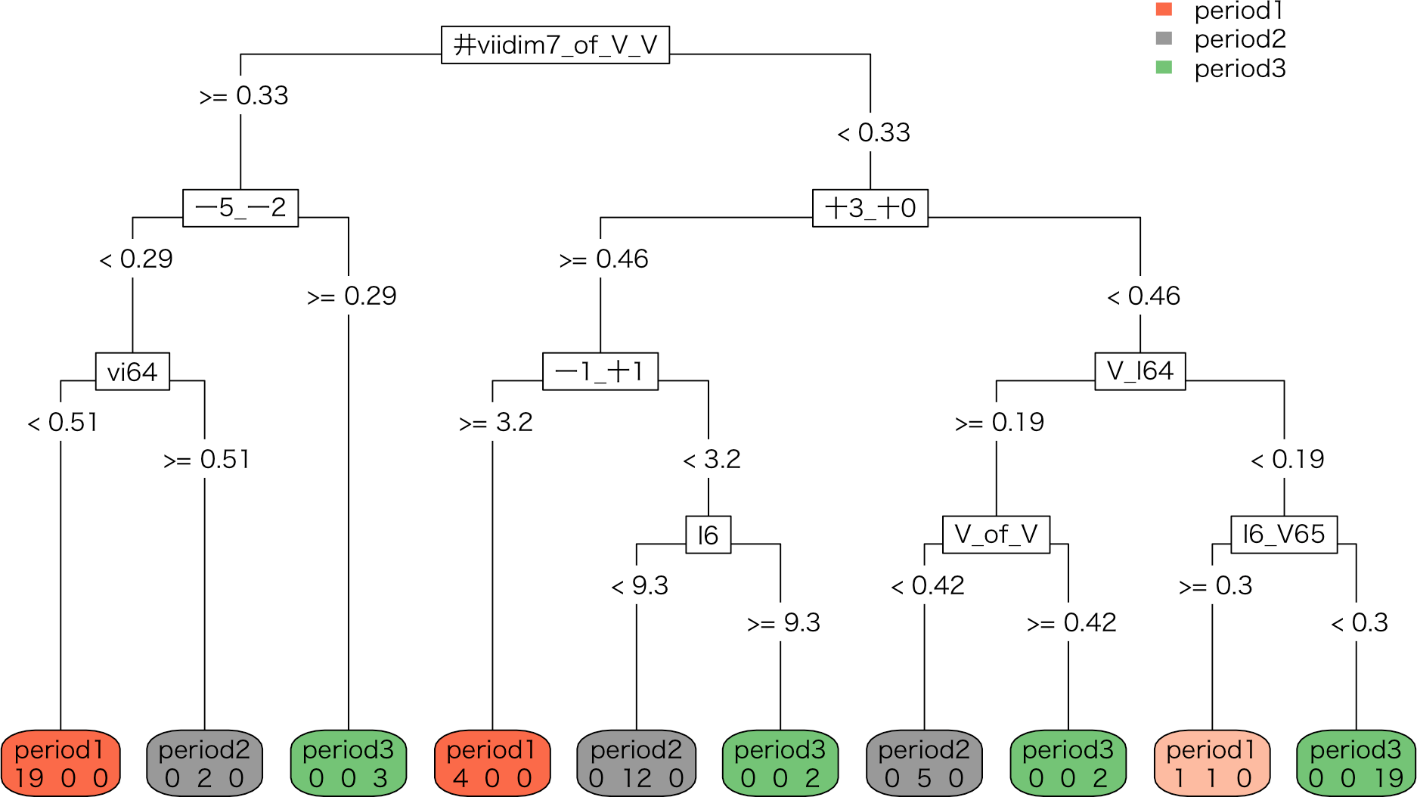
In this study, we found out that the periodisation by Lenz (1855) is a valid classification for the first period and the third period in terms of harmony and melody. However, the misclassifications frequently occur with respect to the second period. The accuracies of two-period-models also indicate that the model performs best when the second period is not involved in the target category.
The question remains as to whether this result can be interpreted as the periodisation criteria for other genres of his music. The precise boundary that separates the last period from the rest of Beethoven’s early career still remains unclear. This is due to the lack of works composed during the 14 years (1810-1825) in which he did not compose any string quartets. This indicates the necessity for further investigation that involves other genres of his music to compensate for this gap. Additionally, future research should compare the accuracy of the models based on several periodisations other than Lenz (1855) in order to ultimately redraw periodisation boundaries that best classifies the works by Beethoven in terms of stylistic evolution.
Bücken, E. (1931). Ludwig van Beethoven. Athenaion.
Hirano, A. (2012). Ludwig van Beethoven (The Great Composers: Life and Works). Ongaku-no-Tomosha.
Honingh, A. and Bod, R. (2011). “Clustering and classification of music by interval categories.” International Conference on Mathematics and Computation in Music. Springer.
Kerman, J., Tyson, A., and Burnham, S. (2001). “Beethoven.” The New Grove Dictionary of Music and Musicians. 2nd ed. Macmillan.
Lenz, W. v. (1855). Beethoven et Ses Trois Styles. Wentworth Press.
Moroi, S. (1983). Beethoven’s Piano Sonata: Study on Composition. Ongaku-no-Tomosha.
Neuwirth, M., Harasim, D., Moss, F.C., and Rohrmeier, M. (2018). “The Annotated Beethoven Corpus (ABC): A Dataset of Harmonic Analyses of All Beethoven String Quartets.” Frontiers Digital Humanities, 5(16).
Richard, M. C. (2011). “Analyzing Tension and Drama in Beethoven’s First-Movement Sonata Forms.” PhD diss. University of Toronto.
Schenk, E. (1967). “Ausgewählte Aufsätze, Reden und Vorträge.” Wiener musikwissenschaftliche Beiträge 7. Graz.